Motion Capture Interpolation

Reconstructing missing motion capture frames using different interpolation techniques
Pranav Rathod

Date: March 12, 2025

In this project for my CSCI 520 course, I set out to improve the smoothness and naturalness of motion capture animations by implementing various interpolation techniques. Working with ASF/AMC motion capture data—where the ASF file defines the skeleton structure and the AMC file records joint rotations and root translations at 120 frames per second—I explored four distinct methods:

• Linear Euler Interpolation
• Bezier Euler Interpolation
• SLERP Quaternion Interpolation
• Bezier SLERP Quaternion Interpolation

Overview

The goal was to generate keyframes by periodically dropping every N-th frame from the original motion data, and then reconstruct the full motion sequence by interpolating between these keyframes. I compared both Euler-based and quaternion-based methods to assess their performance in reducing abrupt transitions and preserving motion continuity. I also created detailed graphs and videos that visually compare the various interpolation techniques.

Video Demonstration and Source Code

To further validate the results, I created three videos using the martial arts dataset (135_06-martialArts.amc) with N=40:

Each video uses the default camera settings and distinguishes the input motion (in red) from the interpolated output (in green). You can find all the source code, graphs, and videos in the GitHub repository: GitHub Repository.

Conversion Routines

• Euler to Rotation Matrix & Back:
  The functions Euler2Rotation() and Rotation2Euler() (implemented in interpolator.cpp) convert between Euler angles (in degrees) and a 3×3 rotation matrix. These routines are critical because the conversion to a rotation matrix is a stepping stone for converting to quaternions while preserving the correct order (XYZ) of rotations.

• Euler to Quaternion & Quaternion to Euler:
  The Euler2Quaternion() function first converts Euler angles to a rotation matrix and then uses the provided quaternion library (see quaternion.cpp and quaternion.h) to convert that matrix into a unit quaternion. This approach avoids the pitfalls of gimbal lock that are inherent to Euler representations. Conversely, Quaternion2Euler() converts a quaternion back to Euler angles by first converting the quaternion to a rotation matrix and then applying Rotation2Euler().

Interpolation Methods

• Linear Interpolation:
  In Euler space, linear interpolation is performed by simply taking a weighted sum of the starting and ending Euler angles for each bone (see LinearInterpolationEuler() in interpolator.cpp). However, because Euler angles do not behave linearly under rotation, this method can lead to abrupt changes.
  For quaternion-based linear interpolation, the implementation uses the SLERP (Spherical Linear Interpolation) function. The function Slerp() computes the interpolation by ensuring that the motion follows the shortest path on the unit sphere, thereby maintaining a constant angular velocity and yielding smoother rotations.

• Bezier Interpolation:
  To further smooth the interpolation, I implemented Bezier interpolation methods for both Euler and quaternion representations.

  • Euler Bezier Interpolation:
    The approach computes control points for each segment using a 1/3 factor based on neighboring keyframes. These control points are then used in the De Casteljau algorithm (implemented in DeCasteljauEuler()) to generate a smooth curve between keyframes. This method tends to reduce abrupt transitions compared to linear interpolation, though it is still limited by the properties of Euler angles.
  • Quaternion Bezier (Bezier SLERP) Interpolation:
    Here, the idea is extended to quaternion space. Since quaternions represent rotations more naturally, this method applies SLERP at each step of the De Casteljau algorithm (see DeCasteljauQuaternion()) to interpolate between quaternions. Control points in quaternion space are computed using modified SLERP steps as well as a dedicated function Double(), which calculates an intermediate quaternion using the dot product between two quaternions. This careful adjustment of control points helps maintain continuity in acceleration and provides the smoothest transitions among all methods.

Driver and File Processing

• Motion and Skeleton Classes:
  The Motion and Skeleton classes (see motion.h, motion.cpp, and skeleton.h) handle loading, processing, and writing the ASF and AMC files. The Motion class stores a sequence of postures (each containing root positions and bone rotations) which are then modified by the interpolator.

• Interpolation Driver:
  The file interpolate.cpp serves as the driver application that combines all components. It parses command-line arguments, loads the appropriate ASF and AMC files, selects the interpolation method based on user input, and writes the interpolated motion back to an AMC file. This modularity makes it straightforward to test different methods (e.g., linear vs. Bezier, Euler vs. Quaternion).

Visualization and Analysis

The mocapPlayer (source files mocapPlayer.cpp and mocapPlayer.h) is used to visualize both the original and interpolated motions. By overlaying the two motions (with distinct colors for clarity), I was able to generate comparative videos that clearly illustrate the smoother transitions achieved by quaternion-based methods over the Euler-based ones.

Additionally, I plotted four graphs comparing the different techniques:

• Graph #1: Linear Euler vs. Bezier Euler for the lfemur X-axis (frames 600–800, N=20)

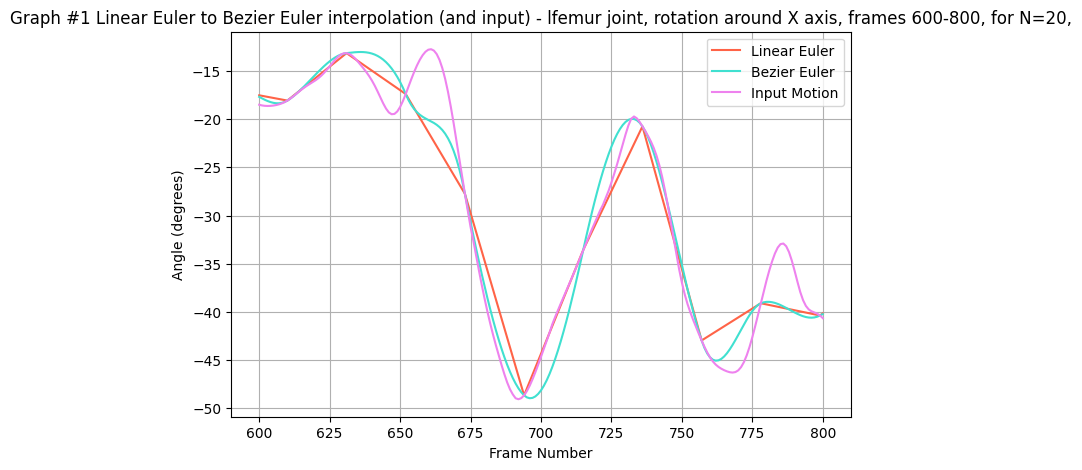
• Graph #2: SLERP Quaternion vs. Bezier SLERP Quaternion for the lfemur X-axis (frames 600–800, N=20)

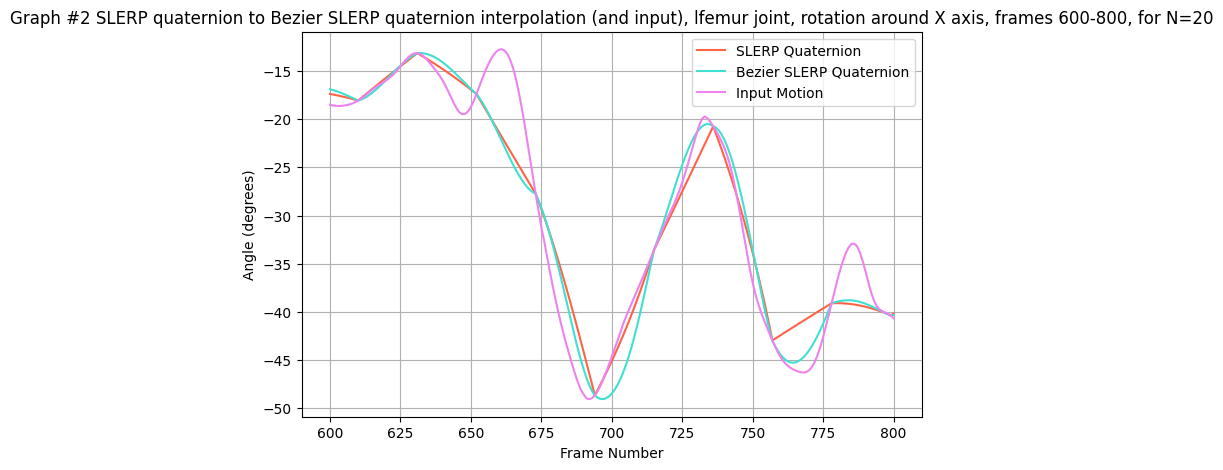
• Graph #3: Linear Euler vs. SLERP Quaternion for root rotation around the Z-axis (frames 200–500, N=20)

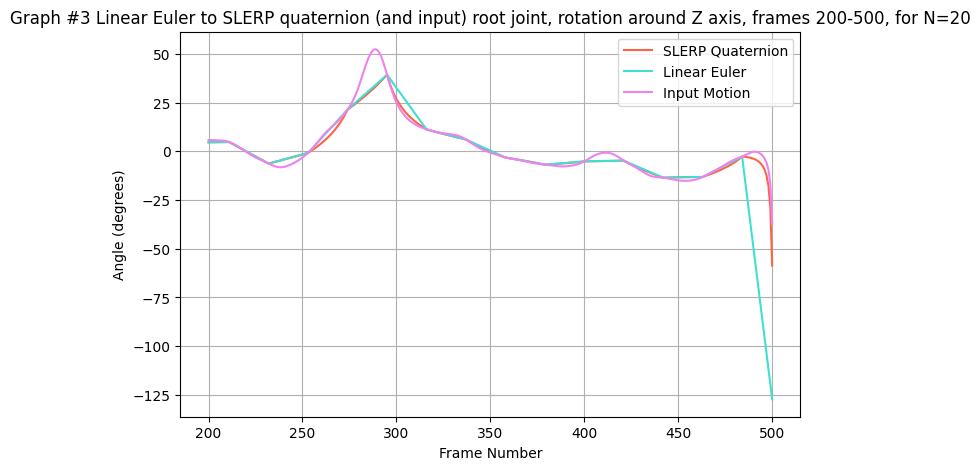
• Graph #4: Bezier Euler vs. Bezier SLERP Quaternion for root rotation around the Z-axis (frames 200–500, N=20)

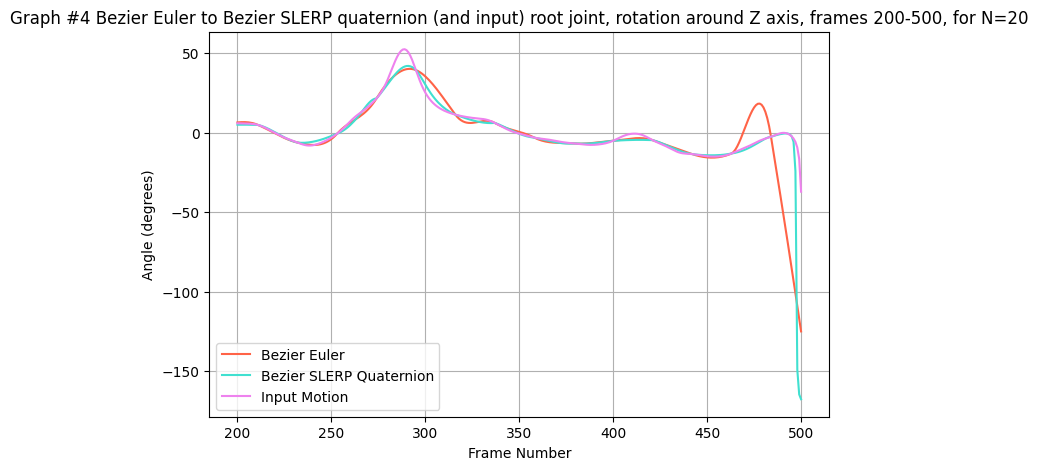
The graphs demonstrate that while both Bezier curves smooth the data better than their linear counterparts, the quaternion methods (especially Bezier SLERP) more faithfully preserve the original motion characteristics without the risk of gimbal lock.

Reflections

This project was both challenging and rewarding. Through the implementation, I gained a deeper understanding of:

• Why Euler-based interpolation can lead to unnatural motion and how the non-linearities in rotation can cause abrupt changes.
• How quaternion-based interpolation, especially when augmented with Bezier smoothing (Bezier SLERP), provides a more natural representation of rotational motion.
• The importance of proper conversion routines between Euler angles, rotation matrices, and quaternions.

Overall, the exercise not only honed my programming and mathematical skills but also reinforced the importance of leveraging advanced interpolation techniques for realistic computer animations. I look forward to further applying these techniques in future projects.